1、掌握概率、条件概率的概念,并会计算简单的概率、条件概率。
概率,亦称“或然率”,它是反映随机事件出现的可能性大小。随机事件是指在相同条件下,可能出现也可能不出现的事件。例如,从一批有正品和次品的商品中,随意抽取一件,“抽得的是正品”就是一个随机事件。设对某一随机现象进行了n次试验与观察,其中A事件出现了m次,即其出现的频率为m/n。经过大量反复试验,常有m/n越来越接近于某个确定的常数(此论断证明详见伯努利大数定律)。该常数即为事件A出现的概率,常用P (A) 表示。
条件概率是指事件A在事件B发生的条件下发生的概率。条件概率表示为:P(A|B),读作“A在B发生的条件下发生的概率”。若只有两个事件A,B,那么,P(A|B)=P(AB)/P(B)。
P(B|A)=P(A|B)P(B)/P(A)
统计独立性
当且仅当两个随机事件A与B满足P(A∩B)=P(A)P(B)的时候,它们才是统计独立的,这样联合概率可以表示为各自概率的简单乘积。
同样,对于两个独立事件A与B有P(A|B)=P(A)以及P(B|A)=P(B),换句话说,如果A与B是相互独立的,那么A在B这个前提下的条件概率就是A自身的概率;同样,B在A的前提下的条件概率就是B自身的概率。
互斥性
当且仅当A与B满足P(A∩B)=0且P(A)≠0,P(B)≠0的时候,A与B是互斥的。
因此,P(A|B)=0,P(B|A)=0。换句话说,如果B已经发生,由于A不能和B在同一场合下发生,那么A发生的概率为零;同样,如果A已经发生,那么B发生的概率为零。
2、理解随机事件的独立性和随机变量的独立性。
事件的相互独立可定义试验的相互独立,试验的相互独立可推出一些事件的相互独立。试验的独立性和随机变量的独立性都是在事件独立性的基础上来定义的。随机变量取某个值或取某个连续区间时,就是表示某事件。
3、掌握乘法公式、全概率公式、贝叶斯公式,并会简单应用。



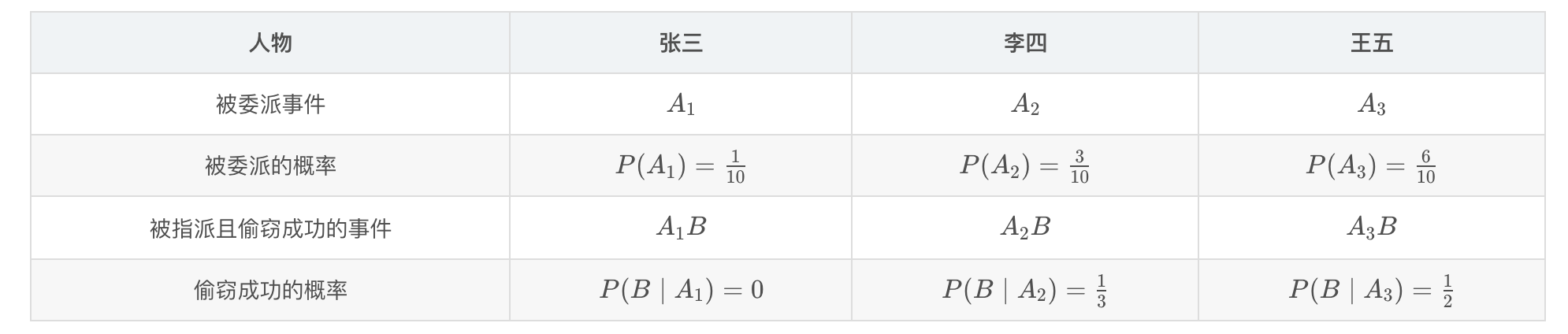

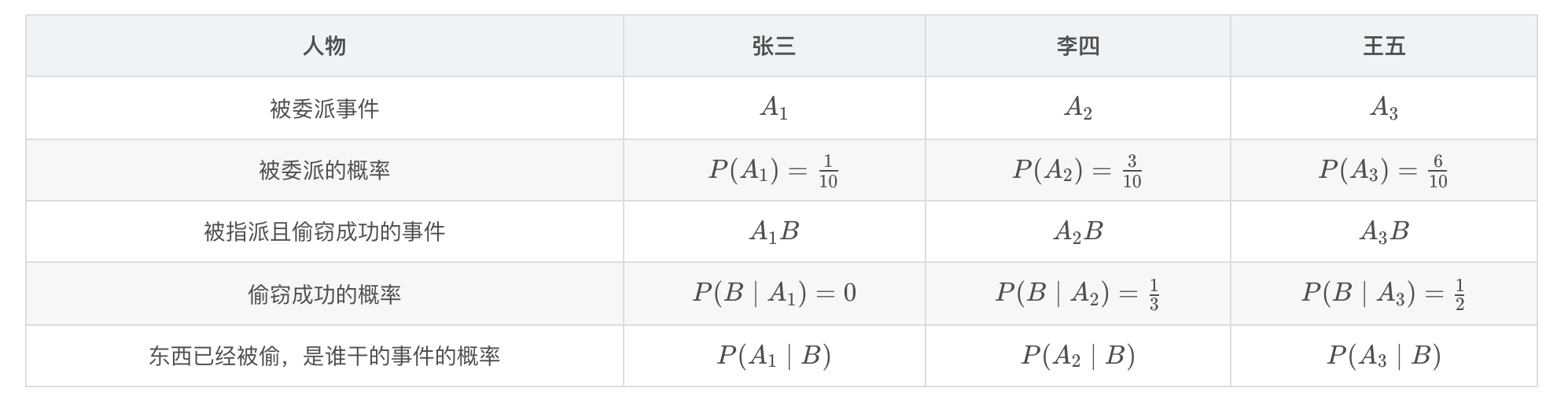
4、掌握随机变量分布函数的概念,掌握连续型随机变量的密度函数和离散型随机变量的分布列。
概率分布用以表达随机变量取值的概率规律,根据随机变量所属类型的不同,概率分布取不同的表现形式
离散型分布:二项分布、多项分布、伯努利分布(两点分布)、泊松分布
连续型分布:均匀分布、正态分布、指数分布、伽玛分布、偏态分布、贝塔分布
5、掌握常见分布(两点分布、二项分布、泊松分布、均匀分布、正态分布、指数分布)及其简单性质。
二项分布的每一次尝试都是独立的,前一次投掷的结果不能决定或影响当前投掷的结果,只有两个可能结果并且重复n次的实验叫做二项式。
多项分布是二项分布的推广扩展,在n次独立实验中每次只输出k种结果中的一个,且每种结果都有一个确定概率,多项分布给出在多种输出状态的情况下,关于成功次数的各种组合的概率。
伯努利分布(两点分布)只有两种可能的结果,1-成功和0-失败,具有伯努利分布特征的随机变量X可以取值为1的概率为p,取值为0的概率1-p,其中成功和失败的概率不一定相等。
当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。通常当n≧20,p≦0.05时,就可以用泊松公式近似得计算。
均匀分布也叫矩形分布,它是对称概率分布,在相同长度间隔的分布概率是等可能的。 均匀分布由两个参数a和b定义,它们是数轴上的最小值和最大值,通常缩写为U(a,b)。
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution)。正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。
指数分布(也称为负指数分布)是描述泊松过程中的事件之间的时间的概率分布,即事件以恒定平均速率连续且独立地发生的过程。 这是伽马分布的一个特殊情况。 它是几何分布的连续模拟,它具有无记忆的关键性质。 除了用于分析泊松过程外,还可以在其他各种环境中找到。
6、理解数学期望、方差(标准差)、相关系数的概念,并会简单计算。
数学期望
在概率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小。
方差
概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中,研究方差即偏离程度有着重要意义。方差是衡量源数据和期望值相差的度量值。
标准差
标准差是方差算术平方根。
7、了解多元随机变量的概念,掌握多元正态分布。
多元随即变量也是变量,这个变量有两个未知的数组成
比如说,向直角坐标平面内投掷小球,小球的落点是一个随机变量,这个随机变量是用坐标表示(x,y),则就是二元随机变量
又如某一天的天气情况,由阴晴和风的情况组成,是一个随机变量,用(晴,三级)表示某天的天气晴,三级风,这也是一个二元随机变量,如果再加上温度的话,就是三元随机变量了。
多变量正态分布亦称为多变量高斯分布。它是单维正态分布向多维的推广。它同矩阵正态分布有紧密的联系。
8、理解统计量的概念,理解样本均值、样本方差(标准差)的概念,并会简单计算。
统计量是统计理论中用来对数据进行分析、检验的变量。宏观量是大量微观量的统计平均值,具有统计平均的意义,对于单个微观粒子,宏观量是没有意义的.相对于微观量的统计平均性质的宏观量也叫统计量。需要指出的是,描写宏观世界的物理量例如速度、动能等实际上也可以说是宏观量,但宏观量并不都具有统计平均的性质,因而宏观量并不都是统计量。
9、了解点估计的概念,了解点估计的无偏性、相合性。
10、了解参数的矩估计、最大似然估计。
11、了解线性回归的基本概念。
线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。其表达形式为y = w’x+e,e为误差服从均值为0的正态分布。
回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
12、了解方差分析(ANOVA)的基本概念。
方差分析(Analysis of Variance,简称ANOVA),又称“变异数分析”,是R.A.Fisher发明的,用于两个及两个以上样本均数差别的显著性检验。 由于各种因素的影响,研究所得的数据呈现波动状。造成波动的原因可分成两类,一是不可控的随机因素,另一是研究中施加的对结果形成影响的可控因素。